MINIMAX Algorithm

Introduction

Welcome to today's coding club class! In this session, we will explore the fascinating world of the Minimax algorithm. Minimax is a fundamental concept in game theory and artificial intelligence that enables intelligent decision-making in games. Whether you're interested in building game-playing agents or simply understanding strategic decision-making, the Minimax algorithm is a powerful tool to have in your arsenal. Let's dive in!

1. Understanding the Basics

2. Overview of game theory and decision-making in games.

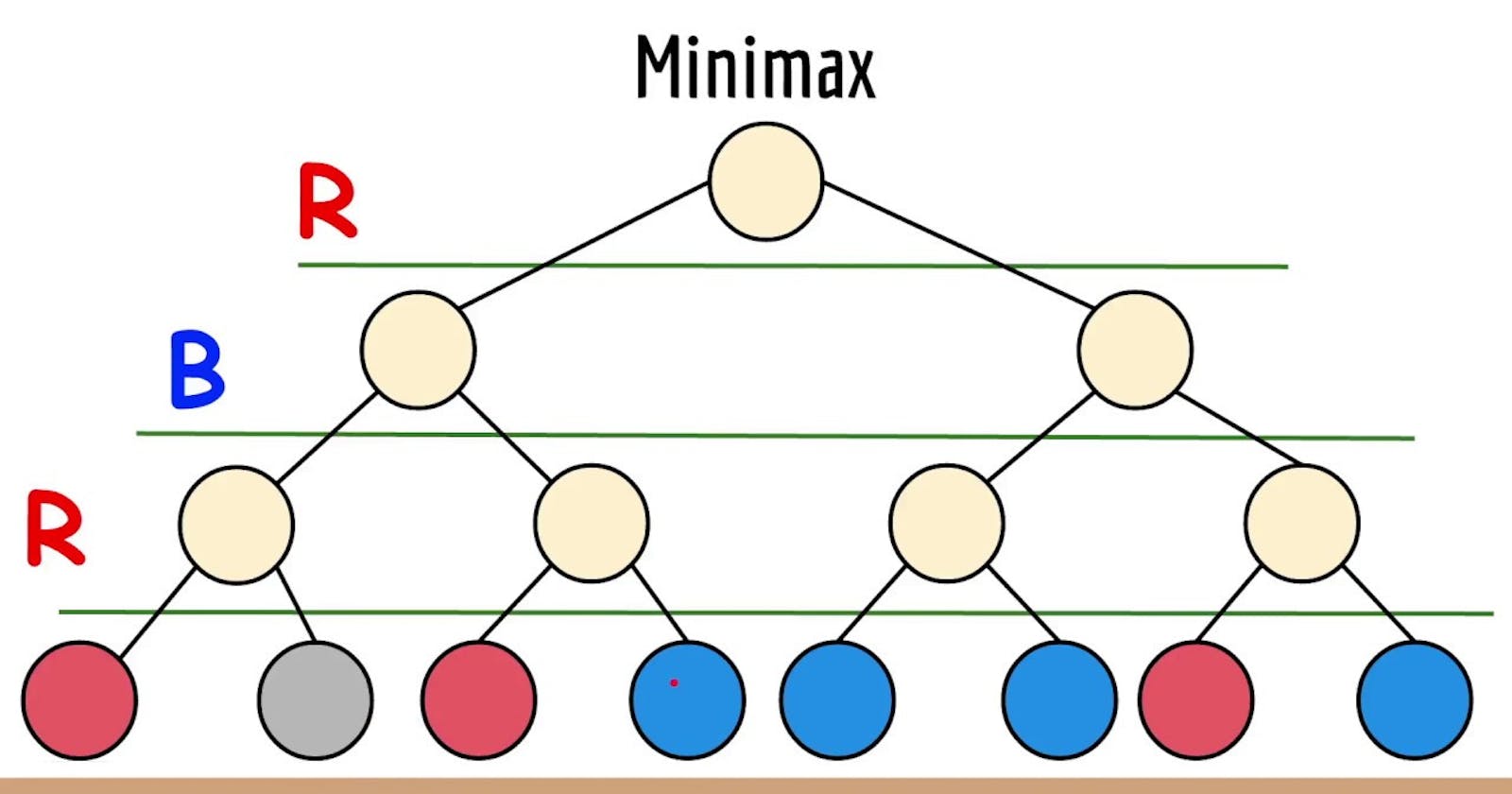
3. Introduction to the Minimax algorithm and its goals.
4. How Minimax works: the concept of game trees and the evaluation function.
5. Exploring the two key players: the maximizing player (Max) and the minimizing player (Min).

6. The idea of searching the game tree and evaluating terminal states.

7. Minimax Algorithm in Action:

8. Implementing Minimax: step-by-step breakdown of the algorithm.

9. Pseudocode representation for clarity.
10. Recursive depth-first search and tree traversal.
11. Minimax with alpha-beta pruning: optimizing the search process.
12. Understanding the alpha and beta values and their role in pruning.

13. Advantages of alpha-beta pruning.

14. Applying Minimax to Practical Scenarios:

15. Tic-Tac-Toe: a classic example to illustrate the Minimax algorithm.

    • Creating the game state representation.
    • Implementing the evaluation function for terminal states.
    • Coding the Minimax algorithm for optimal moves.
    • Testing and playing against the computer agent.

16. Chess, Checkers, or other complex games:

    • Discussing the challenges of applying Minimax to larger games.
    • Strategies for handling the game complexity.
    • Techniques to improve performance and efficiency.

17. Real-World Applications:

18. Beyond games: exploring applications of Minimax in decision-making systems.

19. Robotics, autonomous vehicles, and strategic planning.
20. Minimax in economics, political science, and negotiation scenarios.

21. Limitations and considerations in real-world applications.

22. How Does It Works?

23. Tree Number One:

24. Tree Number Two:

25. MiniMax In Code

def minimax_search(state, game):
    player = game.next_player(state)
    # define labels on each level of the tree
    def max_value(state):
        if game.is_leaf(state):
            return game.goodness(state, player)
        return max([min_value(s) for (_, s) in game.next_state(state)])

    def min_value(state):
        if game.is_leaf(state):
            return game.goodness(state, player)
        return min([max_value(s) for (_, s) in game.next_state(state)])

    # minimax method
    children_values = [(a, min_value(s)) for (a, s) in game.next_state(state)]
    step, value = max(children_values, key=lambda a_s: a_s[1])
    return step

Conclusion

Congratulations! You have successfully completed our Minimax algorithm class. You now have a strong foundation in strategic decision-making and game theory. By implementing the Minimax algorithm, you can create intelligent game-playing agents and tackle complex decision problems. Keep exploring and applying these concepts to unleash the full potential of Minimax in your coding adventures.